Zyklische Gruppe - Wikipedia

In der Algebra ist eine zyklische Gruppe oder monogene Gruppe eine Gruppe, die durch ein einzelnes Element erzeugt wird. ^[1] Das heißt, sie besteht aus einer Gruppe von Elementen mit einem einzige umkehrbare assoziative Operation, und sie enthält ein Element g so dass jedes andere Element der Gruppe durch wiederholtes Anwenden der Gruppenoperation oder deren Inverse auf g erhalten werden kann. Jedes Element kann als Potenz von g in multiplikativer Notation oder als Vielfaches von g in additiver Notation geschrieben werden. Dieses Element g wird als Generator der Gruppe bezeichnet. ^[1]

Jede unendliche zyklische Gruppe ist isomorph zur Additionsgruppe von Z den ganzen Zahlen. Jede endliche zyklische Ordnungsgruppe n ist isomorph zu der Additivgruppe von Z / n Z die ganzen Zahlen modulo n . Jede zyklische Gruppe ist eine abelsche Gruppe (was bedeutet, dass ihre Gruppenoperation kommutativ ist), und jede endlich erzeugte abelsche Gruppe ist ein direktes Produkt von zyklischen Gruppen.

Definition [ edit ]

Die sechs 6. komplexen Wurzeln der Einheit bilden eine zyklische Gruppe unter Multiplikation. z ist ein primitives Element, aber z ² nicht, weil die ungeraden Kräfte von z keine Macht von z ^{sind ] 2} .

Eine Gruppe G wird als zyklisch bezeichnet, wenn ein Element existiert g in G so dass G g {= { g ⁿ | n ist eine Ganzzahl}. Da jede Gruppe, die durch ein Element in einer Gruppe erzeugt wird, eine Untergruppe dieser Gruppe ist, zeigt sich, dass die einzige Untergruppe einer Gruppe G die g g enthält, G selbst ist es genügt zu zeigen, dass G zyklisch ist.

Zum Beispiel, wenn G = { g ⁰ g ¹ g ^{2 g 3 g 4 g 5 5 ist eine Gruppe der Ordnung 6, dann g 6 = g 0 und G ist zyklisch. In der Tat ist G im Wesentlichen das Gleiche wie (dh isomorph) zu der Menge {0, 1, 2, 3, 4, 5} mit dem Zusatz modulo 6. Zum Beispiel 1 + 2 × 3 (mod 6) entspricht g 1 g 2 = g 3 und 2 + 5 ≡ 1 (mod 6) entspricht g 2 · g 5 = g 7 = g 1 und so weiter. Man kann den Isomorphismus verwenden, definiert durch [( g i ) = i .}

Der Name "zyklisch" kann irreführend sein: ^[2] Es ist möglich, unendlich viele Elemente zu erzeugen und keine wörtliche Zyklen zu bilden. das heißt, jedes g ⁿ ist verschieden. (Es kann angenommen werden, dass es einen unendlich langen Zyklus hat.) Eine auf diese Weise erzeugte Gruppe (z. B. die erste Friesgruppe, p1) wird als unendliche zyklische Gruppe bezeichnet und ist zum Additiv isomorph Gruppe der ganzen Zahlen, ( Z +) .

Die Sammlung französischer Mathematiker, die unter dem Namen Nicolas Bourbaki publiziert, führte die Bezeichnung monogene Gruppe für eine Gruppe ein, die ein Generatorsystem zuließ, das aus einem einzigen Element bestand, und beschränkte den Begriff "zyklische Gruppe" auf nur begrenzt monogene Gruppen unter Vermeidung des Begriffs "unendliche zyklische Gruppe". ^{[note 1]}

Beispiele [ edit ]

Integer und modulare Addition [ edit

Die Menge der ganzen Zahlen bildet mit der Additionsoperation eine Gruppe. ^[1] Es handelt sich um eine unendliche zyklische Gruppe da alle ganzen Zahlen als endliche Summe oder Differenz von Kopien der Zahl 1 geschrieben werden können. In dieser Gruppe sind 1 und -1 die einzigen Generatoren. Jede unendliche zyklische Gruppe ist zu dieser Gruppe isomorph.

Für jede positive ganze Zahl n bildet die Menge der Ganzzahlen modulo n wiederum mit der Additionsoperation eine endliche zyklische Gruppe, die Gruppe Z /([19459007$n)[19659049$Element g ist ein Generator dieser Gruppe, wenn g relativ zu n steht (weil Diese Elemente können alle anderen Elemente der Gruppe durch Multiplikation der Zahl erzeugen. Somit ist die Anzahl der verschiedenen Generatoren φ ( n ), wobei φ die Euler-Funktion ist, die Funktion, die die Anzahl der Zahlen modulo zählt ] n die relativ zu n stehen. Jede endliche zyklische Gruppe ist isomorph zu einer Gruppe Z / ( n ), wobei n die Ordnung der Gruppe ist.

Die ganzzahligen und modularen Additionsoperationen, die zur Definition der zyklischen Gruppen verwendet werden, sind beide Additionsoperationen kommutativer Ringe und werden auch als Z und Z / ( / [) bezeichnet. ). Wenn p eine Primzahl ist, dann ist Z / ( p ) ein endliches Feld und wird stattdessen als F _{p [19659052] oder GF ( p ). Jedes Feld mit p Elementen ist isomorph zu diesem.}

Modulare Multiplikation [ edit ]

Für jede positive ganze Zahl n ist die Teilmenge der Ganzzahlen modulo n die relativ zu prim n bildet mit der Operation der Multiplikation eine endliche Gruppe, die für viele Werte von n wiederum zyklisch ist. Es ist die Gruppe unter Multiplikation modulo n und sie ist zyklisch, wenn n 1, 2, 4 ist, eine Potenz einer ungeraden Primzahl oder die doppelte Potenz einer ungeraden Primzahl. ^[4] (Sequenz A033948 in der OEIS) ^[5] Seine Elemente sind die Einheiten des Rings Z / n Z ; Es gibt φ ( n ) von denen, wobei wiederum φ die Funktion tient ist. Diese Gruppe wird geschrieben als ( Z / n Z ) ^× . Zum Beispiel (19459003) Z / 6 Z ) ^× hat als Elemente {1,5}; 6 ist zweimal eine Primzahl, also ist dies eine zyklische Gruppe. Im Gegensatz dazu ist (19459003) Z / 8 Z ) ^× (mit Elementen {1,3,5,7}) die Klein-Gruppe und ist nicht zyklisch. Wenn ( Z / n Z ) ^× zyklisch ist, ist jeder Generator (durch Potenzierung) von [ Z / ] n Z ) ^× wird als primitive Wurzelmodulo n bezeichnet.

Die zyklische Gruppe ( Z / p Z ) ^× für eine Primzahl p wird geschrieben ( Z / p Z ) ^* weil es aus Nicht-Null-Elementen des endlichen Ordnungsfeldes p besteht. Allgemeiner ist jede endliche Untergruppe der multiplikativen Gruppe eines Feldes zyklisch. ^[6]

Rotationssymmetrien edit

Die Menge der Rotationssymmetrien eines Polygons bildet eine endliche zyklische Gruppe. ^[7] Wenn es n verschiedene Möglichkeiten gibt, das Polygon durch eine Rotation (einschließlich der Nullrotation) auf sich selbst abzubilden, dann ist diese Gruppe isomorph zu Z _n . In drei oder höheren Dimensionen kann es andere endliche Symmetriegruppen geben, die zyklisch sind, aber nicht den Satz von Rotationen um eine einzelne Achse bilden.

Die Gruppe S ¹ aller Rotationen eines Kreises (die Kreisgruppe) ist nicht zyklisch. Im Gegensatz zur unendlichen zyklischen Gruppe ist es nicht einmal abzählbar. Es gibt auch andere unendliche Rotationsgruppen (z. B. den Rotationssatz nach rationalen Winkeln), die abzählbar sind, aber nicht zyklisch sind.

Galois-Theorie [ edit ]

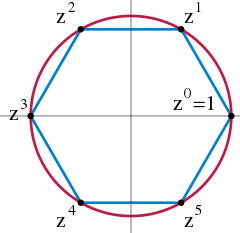
Eine n -te Wurzel der Einheit kann als eine komplexe Zahl betrachtet werden, deren n -te Potenz ist 1. Das heißt, es ist eine Wurzel des Polynoms x ⁿ -1. Die n ten Wurzeln der Einheit bilden eine zyklische Ordnungsgruppe n unter Multiplikation. ^[1] Beispielsweise ist das Polynom 0 = z ³ - 1 Faktoren als ( z - s ⁰ ) ( z - s ¹ ) ( z - s ² ) wobei s = e ^{2 πi / 3} ; Das Set { s ⁰ s ¹ s ² } bildet unter Multiplikation eine zyklische Gruppe. Eine andere Gruppe bildet die Galois-Gruppe der Felderweiterung der rationalen Zahlen, die durch die ten Wurzeln der Einheit erzeugt wurden. Es ist isomorph zu der multiplikativen Gruppe modulo n die Ordnung [ ( n ) hat und für einige, aber nicht alle, n .

Eine Felderweiterung wird als zyklische Erweiterung bezeichnet, wenn ihre Galois-Gruppe eine zyklische Gruppe ist. Die Galois-Gruppe jeder endlichen Ausdehnung eines endlichen Feldes ist endlich und zyklisch, mit einem Iterat des Frobenius-Endomorphismus als Generator. ^[8] Umgekehrt, gegeben eines endlichen Feldes F und einer endlichen zyklischen Gruppe ] G gibt es eine endliche Felderweiterung von F deren Galois-Gruppe G . ^[9]

Untergruppen und Notation ist.

Alle Untergruppen und Quotientengruppen von cyclischen Gruppen sind cyclisch. Insbesondere haben alle Untergruppen von Z die Form m Z wobei m eine ganze Zahl ≥ 0 ist. Alle diese Untergruppen unterscheiden sich voneinander, und abgesehen von der Trivialgruppe (für m = 0 ) sind alle isomorph zu Z . Das Gitter der Untergruppen von Z ist isomorph zu dem durch die Teilbarkeit geordneten dualen Gitter der natürlichen Zahlen. ^[10] Da insbesondere die Primzahlen die Zahlen ohne nicht-trivialen Teiler sind, ist eine zyklische Gruppe einfach wenn und nur dann, wenn ihre Reihenfolge (die Anzahl ihrer Elemente) prim ist ^[11]

Da die zyklischen Gruppen abelian sind, werden sie oft additiv geschrieben und mit Z bezeichnet _n Diese Notation kann jedoch für Zahlentheoretiker problematisch sein, da sie mit der üblichen Notation für p -adische Nummernringe oder Lokalisierung bei einem Primidealideal kollidiert. Die Quotientennotierungen Z / n Z Z / ( n ) und Z / n sind häufig verwendete Alternativen.

Man kann stattdessen die Gruppe multiplikativ schreiben und sie mit C _n angeben, wobei n die Ordnung für endliche Gruppen und C für die unendliche zyklische Gruppe ist. ^{[note 2]} Zum Beispiel g ² g ⁴ = g ¹ in C ₅ 2 + in Z / 5 Z .

Alle Quotientengruppen von Z sind endlich, mit Ausnahme Z / 0 Z = Z / {0}. Für jeden positiven Divisor d von n hat die Quotientengruppe Z / n Z genau eine Untergruppe der Ordnung d die durch die Residuenklasse n / d generierte. Es gibt keine anderen Untergruppen. Unter Verwendung des Quotientengruppenformalismus ist Z / n Z eine Standardnotation für die additive cyclische Gruppe mit n Elementen. In der Ringterminologie ist die Untergruppe n Z auch das Ideal ( n ), daher kann der Quotient auch Z / [ geschrieben werden. n ) ohne Mißbrauch. Diese Alternativen stehen nicht im Widerspruch zur Notation für die p -adischen Ganzzahlen. Die Notation Z / n ist in informellen Berechnungen üblich.

Zusätzliche Eigenschaften [ edit ]

Jede zyklische Gruppe ist abelianisch. ^[1] Das heißt, ihre Gruppenoperation ist kommutativ: gh = hg (für alle g und h in G ). Dies ist klar für die Gruppen der Ganzzahl- und Moduladdition seit r + s [1945 s + r n n ) und es folgt für alle zyklischen Gruppen, da sie alle zu einer durch eine Additionsoperation erzeugten Gruppe isomorph sind. Für eine endliche zyklische Ordnungsgruppe n und jedes Element e der Gruppe ist e ⁿ das Identitätselement der Gruppe . Dies folgt wiederum unter Verwendung des Isomorphismus zur modularen Addition, da kn ≡ 0 (mod n ) für jede ganze Zahl k .

Wenn d ein Divisor von n ist, dann ist die Anzahl der Elemente in Z / n die die Reihenfolge haben. d ist φ ( ), und die Anzahl der Elemente, deren Reihenfolge d d genau ist, ist genau . Wenn G eine endliche Gruppe ist, in der für n > 0 G höchstens n Elemente der Ordnung enthalten n dann G muss zyklisch sein. ^{[note 3]} Die Reihenfolge eines Elements m der Gruppe lautet n / gcd ( n m ).

Das direkte Produkt zweier zyklischer Gruppen Z / n und Z / m m ist n und m sind Coprime. So kann z.B. Z / 12 ist das direkte Produkt von Z / 3 und Z / 4, jedoch nicht das direkte Produkt von Z / 6 und Z / 2. Wenn p eine Primzahl ist, dann ist die einzige Gruppe (bis zum Isomorphismus) mit p Elementen Z / P . Es wird eine primäre zyklische Gruppe genannt. Der fundamentale Satz abelscher Gruppen besagt, dass jede endlich erzeugte abelsche Gruppe das direkte Produkt von endlich vielen endlichen primären zyklischen und unendlichen zyklischen Gruppen ist. Eine Zahl n wird als zyklische Zahl bezeichnet, wenn sie die Eigenschaft hat, dass Z / n die einzige Ordergruppe n ist, die trifft genau zu, wenn gcd ( n φ ( n )) = 1 . ^[13] ist. Die Zahlen enthalten alle Primzahlen , aber auch einige zusammengesetzte Zahlen wie 15 enthalten. Mit Ausnahme von 2 sind jedoch alle zyklischen Zahlen ungerade. Die zyklischen Zahlen sind:

1, 2, 3, 5, 7, 11, 13, 15, 17, 19, 23, 29, 31, 33, 35, 37, 41, 43, 47, 51, 53, 59, 61, 65 67, 69, 71, 73, 77, 79, 83, 85, 87, 89, 91, 95, 97, 101, 103, 107, 109, 113, 115, 119, 123, 127, 131, 133, 137 139, 141, 143, ... (Sequenz A003277 in der OEIS)

Tatsächlich ist eine Zahl n eine zyklische Zahl, wenn und nur gcd ( n φ ( n )) = 1 wobei φ die Funktion des Eulers ist.

Die Definition impliziert sofort, dass zyklische Gruppen eine Gruppenpräsentation haben C _[1945 = ⟨ x | und C _n = ⟨ x | x ⁿ [1945 für endliche n . ^[14]

Zugehörige Objekte edit edit 19659006] edit ]

Die Darstellungstheorie der zyklischen Gruppe ist ein kritischer Basisfall für die Darstellungstheorie allgemeinerer endlicher Gruppen. Im komplexen Fall zerlegt sich eine Darstellung einer zyklischen Gruppe in eine direkte Summe linearer Zeichen, wodurch die Verbindung zwischen Zeichentheorie und Darstellungstheorie transparent wird. Im positiven charakteristischen Fall bilden die nicht zusammensetzbaren Darstellungen der zyklischen Gruppe eine modellhafte und induktive Basis für die Darstellungstheorie von Gruppen mit zyklischen Sylow-Untergruppen und allgemeiner die Darstellungstheorie von Blöcken von zyklischen Defekten.

Zyklusdiagramm [ edit ]

Ein Zyklusgraphen veranschaulicht die verschiedenen Zyklen einer Gruppe und ist besonders nützlich, um die Struktur kleiner endlicher Gruppen zu visualisieren. Ein Zyklusgraph für eine zyklische Gruppe ist einfach ein Kreisgraph, wobei die Gruppenreihenfolge der Anzahl der Knoten entspricht. Ein einzelner Generator definiert die Gruppe als Richtungspfad in der Grafik, und der Inversgenerator definiert einen Rückwärtspfad. Trivialpfade (Identität) können als Schleife gezeichnet werden, werden aber normalerweise unterdrückt. Z ₂ wird manchmal mit zwei gebogenen Kanten als Multigraph gezeichnet. ^[15]

Zyklische Gruppen Z _n Ordnung n , ist ein einzelner Zyklus, der einfach als ein n -seitiges Polygon mit den Elementen an den Scheitelpunkten dargestellt wird. Wenn n = ab wobei a und b relativ hoch sind (dh gcd ( a ) b ) = 1 ), eine zyklische Gruppe Z _n kann in ein direktes Produkt zerlegt werden Z _a × Z _b .

Cayley-Graph [ edit ]

Der Paley-Graph der Ordnung 13, ein umlaufender Graph, der als Cayley-Graph von Z / 13 mit Generatorsatz {1 3,4}

Ein Cayley-Graph ist ein aus einem Paar definierter Graph ( G S ), wobei G eine Gruppe ist und S ist eine Gruppe von Generatoren für die Gruppe; Es hat einen Scheitelpunkt für jedes Gruppenelement und eine Kante für jedes Produkt eines Elements mit einem Generator. Im Fall einer endlichen zyklischen Gruppe mit einem einzelnen Generator ist der Cayley-Graph ein Zyklusgraph, und für eine unendliche zyklische Gruppe mit ihrem Generator ist der Cayley-Graph ein doppelt unendlich langer Pfadgraph. Cayley-Graphen können jedoch auch aus anderen Generatorsätzen definiert werden. Die Cayley-Graphen zyklischer Gruppen mit beliebigen Generatorsätzen werden als Kreisdiagramme bezeichnet. ^[16] Diese Graphen können geometrisch als ein Satz von gleichmäßig beabstandeten Punkten auf einem Kreis oder auf einer Linie dargestellt werden, wobei jeder Punkt mit Nachbarn mit demselben Satz von verbunden ist Entfernungen wie jeder andere Punkt. Es sind genau die vertex-transitiven Graphen, deren Symmetriegruppe eine transitive zyklische Gruppe einschließt. ^[17]

Endomorphismen [ edit

Der Endomorphismusring der abelianischen Gruppe Z n Z ist isomorph zu Z / n Z Z selbst als Ring. ^[18] Unter diesem Isomorphismus ist die Zahl ] r entspricht dem Endomorphismus von Z / n Z der jedes Element der Summe von r Kopien davon zuordnet. Wenn und nur dann, wenn r mit n gemeinsam ist, ist dies eine Bioverbindung, so dass die Automorphismengruppe von Z / n Z isomorph zu der Einheitsgruppe ( Z / n Z ) ^× .

Endomorphismusring der Additivgruppe von Z ist isomorph zum Ring Z . Seine Automorphismengruppe ist isomorph zu der Gruppe von Einheiten des Rings Z d. H. Zu ({- 1, +1}, ×) ≅ C ₂ .

Tensorprodukt und Hom von cyclischen Gruppen [ edit ]

Das Tensorprodukt ${ displaystyle mathbf {z} / m { mathbf {z}} otimes mathbf {z} / n { mathbf {z}} }$